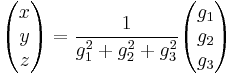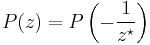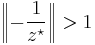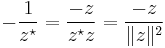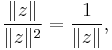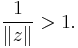Boy's surface

In geometry, Boy's surface is an immersion of the real projective plane in 3-dimensional space found by Werner Boy in 1901 (he discovered it on assignment from David Hilbert to prove that the projective plane could not be immersed in 3-space). Unlike the Roman surface and the cross-cap, it has no singularities (i.e., pinch-points), but it does self-intersect.

To make a Boy's surface:

  1. Start with a sphere. Remove a cap.
  2. Attach one end of each of three strips to alternate sixths of the edge left by removing the cap.
  3. Bend each strip and attach the other end of each strip to the sixth opposite the first end, so that the inside of the sphere at one end is connected to the outside at the other. Make the strips skirt the middle rather than go through it.
  4. Join the loose edges of the strips. The joins intersect the strips.

Boy's surface is discussed (and illustrated) in Jean-Pierre Petit's Le Topologicon.[1]

Boy's surface was first parametrized explicitly by Bernard Morin in 1978. See below for another parametrization, discovered by Rob Kusner and Robert Bryant.

Contents

Symmetry of the Boy's surface

Boy's surface has 3-fold symmetry. This means that it has an axis of discrete rotational symmetry: any 120° turn about this axis will leave the surface looking exactly the same. The Boy's surface can be cut into three mutually congruent pieces.

Model at Oberwolfach

The Mathematical Research Institute of Oberwolfach has a large model of a Boy's surface outside the entrance, constructed and donated by Mercedes-Benz in January 1991. This model has 3-fold rotational symmetry and minimizes the Willmore energy of the surface. It consists of steel strips which represent the image of a polar coordinate grid under a parameterization given by Robert Bryant and Rob Kusner. The meridians (rays) become ordinary Möbius strips, i.e. twisted by 180 degrees. All but one of the strips corresponding to circles of latitude (radial circles around the origin) are untwisted, while the one corresponding to the boundary of the unit circle is a Möbius strip twisted by three times 180 degrees — as is the emblem of the institute (Mathematisches Forschungsinstitut Oberwolfach 2008).

Applications

Boy's surface can be used in sphere eversion, as a half-way model. A half-way model is an immersion of the sphere with the property that a rotation interchanges inside and outside, and so can be employed to evert (turn inside-out) a sphere. Boy's (the case p = 3) and Morin's (the case p = 2) surfaces are beginning of a sequence of half-way models with higher symmetry first proposed by George Francis, indexed by the even integers 2p (for p odd, these immersions can be factor through a projective plane). Kusner's parametrization yields all these.

Parametrization of Boy's surface

Boy's surface can be parametrized in several ways. One parametrization,[2] discovered by Rob Kusner and Robert Bryant, is the following: given a complex number z whose magnitude is less than or equal to one (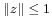\scriptstyle \| z \| \;\le\; 1), let

\begin{align} g_1 &= -{3 \over 2} \mathrm{Im} \left[ {z (1 - z^4) \over z^6 %2B \sqrt{5} z^3 - 1} \right]\\ g_2 &= -{3 \over 2} \mathrm{Re} \left[ {z (1 %2B z^4) \over z^6 %2B \sqrt{5} z^3 - 1} \right]\\ g_3 &= \mathrm{Im} \left[ {1 %2B z^6 \over z^6 %2B \sqrt{5} z^3 - 1} \right] - {1 \over 2}\\ \end{align}

so that

\begin{pmatrix}x\\ y\\ z\end{pmatrix} = \frac{1}{g_1^2 %2B g_2^2 %2B g_3^2} \begin{pmatrix}g_1\\ g_2\\ g_3\end{pmatrix}

where x, y, and z are the desired Cartesian coordinates of a point on the Boy's surface.

If one performs an inversion of this parametrization centered on the triple point, one obtains a complete minimal surface with three "ends" (that's how this parametrization was discovered naturally). This implies that the Bryant-Kusner parametrization of Boy's surfaces is "optimal" in the sense that it is the "least bent" immersion of a projective plane into three-space.

Property of Bryant-Kusner parametrization

If z is replaced by the negative reciprocal of its complex conjugate, 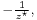\scriptstyle -{1 \over z^\star}, then the functions g1, g2, and g3 of z are left unchanged.

Relating the Boy's surface to the real projective plane

Let 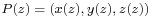\scriptstyle P(z) \;=\; (x(z),\, y(z),\, z(z)), where 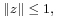\scriptstyle \| z \| \;\le\; 1, denote a point on Boy's surface. Then

P(z) = P\left( -{1 \over z^\star} \right)

but only if 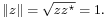\scriptstyle \| z \| \;=\; \sqrt{z z^\star} \;=\; 1. What if 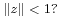\scriptstyle \| z \| \;<\; 1�? Then

\left\| - {1 \over z^\star} \right\| > 1

because

- {1 \over z^\star} = {- z \over z^\star z} = {-z \over \| z \|^2}

whose magnitude is

{\| z \| \over \| z \|^2} = {1 \over \| z \|},

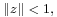but \scriptstyle \| z \| \;<\; 1, so that

{1 \over \| z \|} > 1.

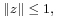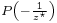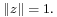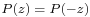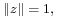Since P(z) belongs to the Boy's surface only when \scriptstyle \|z\| \;\le\; 1,, this means that \scriptstyle P\left( -{1 \over z^\star} \right) belongs to Boy's surface only if \scriptstyle \| z \| \;=\; 1. Thus \scriptstyle P(z) \;=\; P(-z) if \scriptstyle \| z \| \;=\; 1, but all other points on the Boy's surface are unique. The set of complex values 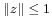\scriptstyle \|z\| \;\le\; 1 is the unit disk, Thus the Boy's surface has been parametrized by a disk such that pairs of diametrically opposite points on the perimeter of the disk are equivalent. Therefore the Boy's surface is homeomorphic to the real projective plane, RP2.

References

  1. ^ Jean-Pierre Petit, Le Topologicon
  2. ^ Bryant, Robert (1988), "Surfaces in conformal geometry", The mathematical heritage of Hermann Weyl (May 12–16, 1987, Duke University, Durham, North Carolina), Proc. Sympos. Pure Math., 48, Providence, RI: Amer. Math. Soc., pp. 227–240 

External links